Insertion Sort
2번째 원소부터 시작하여 i-1(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입하여 정렬하는 알고리즘이다.


최선의 경우 O(N)이라는 엄청나게 빠른 효율성을 가지고 있어, 다른 정렬 알고리즘의 일부로 사용될 만큼 좋은 정렬 알고리즘이다.
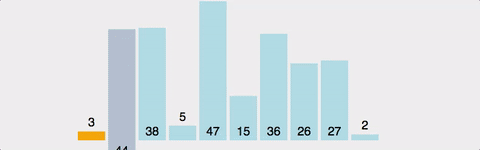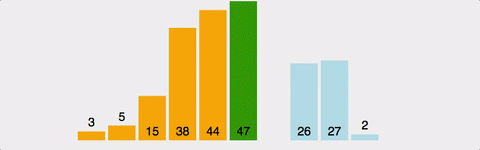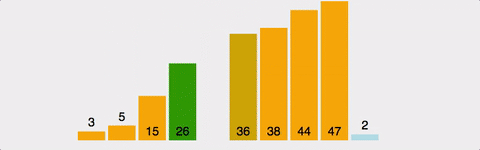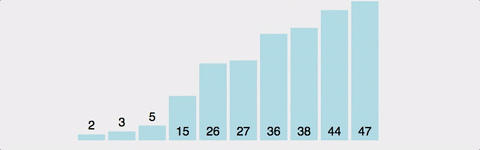

예제 1
public int[] solution(int[] arr) {
if (arr == null) return null;
int temp;
for (int i = 1; i < arr.length; i++) {
temp = arr[i];
int k;
for (k = i - 1; k >= 0; k--) {
if (temp >= arr[k]) {
break;
}
arr[k + 1] = arr[k];
}
arr[k + 1] = temp;
}
return arr;
}예제 2
void insertionSort(int[] arr)
{
for(int index = 1 ; index < arr.length ; index++){ // 1.
int temp = arr[index];
int prev = index - 1;
while( (prev >= 0) && (arr[prev] > temp) ) { // 2.
arr[prev+1] = arr[prev];
prev--;
}
arr[prev + 1] = temp; // 3.
}
System.out.println(Arrays.toString(arr));
}시간복잡도

최악의 경우(역으로 정렬되어 있을 경우), (n-1) + (n-2) +.... + 2 + 1 => n(n-1)/2 즉, O(n^2).
모두 정렬이 되어있는 경우, 한 번씩 밖에 비교를 안 하므로 O(n)의 시간 복잡도를 가지게 된다. 또한, 이미 정렬되어 있는 배열에 자료를 하나씩 삽입/제거하는 경우에는, 현실적으로 최고의 정렬 알고리즘이 되는데, 탐색을 제외한 오버헤드가 매우 적기 때문이다.
최선의 경우는 O(n) 의 시간 복잡도를 갖고, 평균과 최악의 경우 O(n^2) 의 시간복잡도를 갖게 된다.
| Space Complexity | Time Complexity |
| O(1) | O(n^2) |
장점
- 알고리즘이 단순하다.
- 대부분의 원소가 이미 정렬되어 있는 경우, 매우 효율적일 수 있다.
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
- 안정 정렬(Stable Sort)이다.
- Selection Sort나 Bubble Sort과 같은 O(n^2) 알고리즘에 비교하여 상대적으로 빠르다.
단점
- 평균과 최악의 시간 복잡도가 O(n^2)으로 비효율적이다.
- Bubble Sort와 Selection Sort와 마찬가지로, 배열의 길이가 길어질수록 비효율적이다.
참고자료
삽입 정렬 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 삽입 정렬(揷入整列, insertion sort)은 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬
ko.wikipedia.org
삽입 정렬(Insertion Sort) | 👨🏻💻 Tech Interview
삽입 정렬(Insertion Sort) Goal Insertion Sort에 대해 설명할 수 있다. Insertion Sort 과정에 대해 설명할 수 있다. Insertion Sort을 구현할 수 있다. Insertion Sort의 시간복잡도와 공간복잡도를 계산할 수 있다. In
gyoogle.dev
GitHub - JaeYeopHan/Interview_Question_for_Beginner: Technical-Interview guidelines written for those who started studying progr
:boy: :girl: Technical-Interview guidelines written for those who started studying programming. I wish you all the best. :space_invader: - GitHub - JaeYeopHan/Interview_Question_for_Beginner: Techn...
github.com
'CS > 알고리즘' 카테고리의 다른 글
| 이진탐색 - Lower bound, Upper bound (0) | 2023.04.19 |
|---|---|
| 이진탐색 (0) | 2023.04.17 |
| [DP] 한 칸씩 이동하여 최대 합 구하기. (0) | 2022.12.19 |
| [Sort] 거품 정렬 (Bubble Sort | Java) (0) | 2022.10.14 |